Mathematics is fundamental to the formulation and analysis of scientific theories, is a rich and independent field of inquiry, and its study is excellent preparation for life in our highly specialized society. Active research throughout the mathematical subdisciplines, spurred on in part by advances in computing technology, leads to new perspectives and applications. The major in mathematics combines broad study of fundamental theories with in-depth investigation of particular subjects chosen from pure, applied and computational mathematics. A degree in mathematics, either alone or in combination with study in another field, is excellent preparation for careers in industry, universities and research institutes.
Statistics is the science of collecting and analyzing data. Statisticians interact with researchers in all the various disciplines of science, engineering, medicine, social science and business to develop scientifically sound methods in those areas. Most course work in the department is devoted to understanding current methods and the reasoning behind them. A degree in statistics prepares students for careers in industry, government, universities and research institutes, as well as being excellent preparation for professional programs in medicine, law, business administration and public policy and administration.
A beginning student who wishes to take MATH 163 or a more advanced course must have College Board Advanced Placement scores as described in the Admissions section of the catalog.
A student who wishes to enroll in a course requiring a prerequisite must earn a grade of C (not C-) or better in the prerequisite course.
A student’s preparation determines the starting course in any sequence.
Elementary education students not prepared for MATH 111 will begin with MATH 100.
1. Credit not allowed for both MATH 162 and 180.
2. Credit not allowed for both MATH 163 and 181.
3. Credit not allowed for both MATH 314 and 321.
4. Credit not allowed for both MATH 401 and 501.
5. Credit not allowed for both MATH 322 and 422.
6. Students who have credit for any courses numbered MATH 121 and above may not take IS-M 100 or MATH 120 for credit.
7. Students who have credit for any courses numbered 162 and above may not take MATH 120, 121, 123 or 150 for credit. (Students with MATH 180/181 may take MATH 123 for credit).
8. A student may not take an examination to validate credit in mathematics courses except those offered through UNM Testing Center.
9. Mathematics or Statistics course work dating back more than five years cannot automatically be counted as fulfillment of a prerequisite. Students with older course work who feel they have retained subject knowledge are encouraged to take the COMPASS placement tests offered through the University of New Mexico Testing Center.
Courses
MATH 106.
Problems in Intermediate Algebra.
(1)
Study session for 120 with an emphasis on problem solving. (I)
Offered on a CR/NC basis only.
{Fall, Spring}
MATH 107.
Problems in College Algebra.
(1)
Study session for 121 with an emphasis on problem solving. (I)
Offered on a CR/NC basis only.
{Fall, Spring}
MATH 110.
Problems in Elements of Calculus.
(1)
Study session for 180 with an emphasis on problem-solving. (I)
Offered on a CR/NC basis only.
{Fall, Spring}
MATH 111.
Mathematics for Elementary and Middle School Teachers I.
(3)
Course offers an in-depth look at the representations of rational numbers, including base-ten and decimal numbers, integers, fractions, and arithmetic operations on these sets. Problem solving is emphasized throughout. (T)
Prerequisite: 120 or 121 or 123 or 150 or 162 or 180 or STAT 145 or ISM 100 or ACT=>19 or SAT=>450 or Compass Pre-Algebra >56 or Algebra >33
MATH 112.
Mathematics for Elementary and Middle School Teachers II.
(3)
This course develops basic geometric concepts including rigid transformations and congruence; dilations and similarity; length, area and volume; systems of measurement and unit conversions; connections to coordinate geometry. Problem solving is emphasized throughout. (T)
Prerequisite: 111
MATH 116.
Topics in Pre-calculus Mathematics.
(3)
Selected topics from algebra, geometry and trigonometry. (I)
Restriction: permission of the department.
Offered on a CR/NC basis only.
MATH 120.
Intermediate Algebra.
(3)
Note: See Restrictions earlier in Mathematics and Statistics.
Preparation for MATH 121, 129 and STAT 145. Covers linear equations and inequalities, polynomials, factoring, exponents, radicals, fractional expressions and equations, quadratic equations, perimeters, areas of simple geometric shapes, and logarithms. Emphasis on problem solving skills. Acceptable as credit toward graduation, but not acceptable to satisfy UNM core or group requirements. (I)
Prerequisite: ACT=>19 or SAT=>450 or ISM 100 or Compass Pre-Algebra >56 or Algebra >33
MATH 121.
College Algebra.
(3)
Note: See Restrictions earlier in Mathematics and Statistics.
Preparation for MATH 150 and 180. The study of equations, functions and graphs, especially linear and quadratic functions. Introduction to polynomial, rational, exponential and logarithmic functions. Applications involving simple geometric objects. Emphasizes algebraic problem solving skills. Meets New Mexico Lower-Division General Education Common Core Curriculum Area II: Mathematics (NMCCN 1113). (I)
Prerequisite: ACT=>22 or SAT=>510 or MATH 120 or Compass Algebra >54 or College Algebra >33.
MATH 123.
Trigonometry.
(3)
Note: See Restrictions earlier in Mathematics and Statistics.
Definition of the trigonometric functions, radian and degree measure, graphs, basic trigonometric identities, inverse trigonometric functions, complex numbers, polar coordinates and graphs, vectors in 2 dimensions. May be taken concurrently with MATH 150. Meets New Mexico Lower-Division General Education Common Core Curriculum Area II: Mathematics (NMCCN 1113). (I)
Prerequisite: ACT=>25 or SAT=>570 or MATH 121 or Compass College Algebra >54.
MATH 129.
A Survey of Mathematics.
(3)
An introduction to some of the great ideas of mathematics, including logic, systems of numbers, sequences and series, geometry and probability. Emphasizes general problem-solving skills. Meets New Mexico Lower-Division General Education Common Core Curriculum Area II: Mathematics. (I)
Prerequisite: ACT=>22 or SAT=>510 or MATH 120 or 121 or 123 or 150 or 162 or 163 or 180 or 181 or 264.
MATH 150.
Pre-Calculus Mathematics.
(3)
Note: See Restrictions earlier in Mathematics and Statistics.
In-depth study of polynomial, rational, exponential and logarithmic functions and their graphs. Includes the fundamental theorem of algebra, systems of equations, conic sections, parametric equations and applications in geometry. Exploration of the graphing calculator. May be taken concurrently with MATH 123. Meets New Mexico Lower-Division General Education Common Core Curriculum Area II: Mathematics. (I)
Prerequisite: ACT=>25 or SAT=>570 or MATH 121 or Compass College Algebra >54.
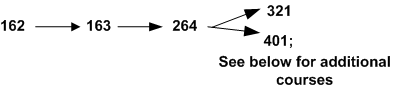
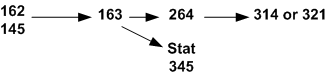
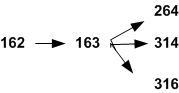
MATH 162.
Calculus I.
(4)
Note: See Restrictions earlier in Mathematics and Statistics.
Derivative as a rate of change, intuitive, numerical and theoretical concepts, applications to graphing, linearization and optimization. Integral as a sum, relation between integral and derivative, and applications of definite integral. Meets New Mexico Lower-Division General Education Common Core Curriculum Area II: Mathematics (NMCCN 1614). (I)
Prerequisite: (ACT=28-31 or SAT=640-700 or MATH 150 or Compass College Algebra >66) and (MATH 123 or Compass Trig >59) or (ACT=>32 or SAT=>700)
MATH 163.
Calculus II.
(4)
Note: See Restrictions earlier in Mathematics and Statistics.
Transcendental functions, techniques of integration, numerical integration, improper integrals, sequences and series with applications, complex variables and parmetrization of curves. (I)
Prerequisite: MATH 162.
MATH 180.
Elements of Calculus I.
(3)
Note: See Restrictions earlier in Mathematics and Statistics.
Limits of functions and continuity, intuitive concepts and basic properties; derivative as rate of change, basic differentiation techniques; application of differential calculus to graphing and minima-maxima problems; exponential and logarithmic functions with applications. Meets New Mexico Lower-Division General Education Common Core Curriculum Area II: Mathematics (NMCCN 1613). (I)
Prerequisite: ACT=>26 or SAT=>600 or MATH 121 or MATH 150 or Compass College Algebra >66.
MATH 181.
Elements of Calculus II.
(3)
Note: See Restrictions earlier in Mathematics and Statistics.
Includes the definite integral, multivariate calculus, simple differential equations, basic review of trigonometry and its relation to calculus. (I)
Prerequisite: 180
MATH 215.
Mathematics for Elementary and Middle School Teachers III.
(3)
Algebra from the viewpoint of the elementary curriculum with emphasis on proportional and linear relationships. Also included: topics from probability and statistics with connections to other topics in the elementary curriculum. Problem solving is emphasized throughout. (T)
Prerequisite: 112
MATH 264.
Calculus III.
(4)
Vector operations, vector representation of planes and curves, functions of several variables, partial derivatives, gradient, tangent planes, optimization, multiple integrals in Cartesian cylindrical and spherical coordinates, vector fields, line integrals and Green’s theorem. (I)
Prerequisite: C (not C-) or better in 163.
MATH 275.
Honors Calculus.
(3)
Differential and integral calculus with an emphasis on conceptual understanding. (I)
Prerequisite: Grade of at least A- in 180 or 162
MATH 300 / 500.
Computing in the Mathematics Curriculum.
(3)
Use of computers and graphing utilities in the mathematics classroom. Introduction to hardware and commercial software. Applications of selected programming languages to the teaching of mathematics. (T)
Prerequisite: 162 or 181
MATH 301 / 503.
Calculus for Teachers.
(3)
A penetrating look at functions, derivatives, intergrals, and the Fundamental Theorem of Calculus that makes explicit how topics in the secondary school curriculum come to fruition in this foundational subject. (T)
Prerequisite: 163
Restriction: permission of instructor
MATH 305 / 507.
Mathematics from a Historical Perspective.
(3)
A survey of mathematical developments prior to 1800; emphasis on problem solving techniques; comparison of older and more modern methods. (T)
Prerequisite: 163
{Fall}
MATH 306 / 506.
College Geometry.
(3)
An axiomatic approach to fundamentals of geometry, both Euclidean and non-Euclidean. Emphasis on historical development of geometry. (T)
{Spring}
MATH 308 / 508.
Theory and Practice of Problem Solving.
(3)
An experience in mathematical invention and discovery at the level of high school geometry and algebra that includes a deeper look at sequences, series, and recursions. (T)
Prerequisite: 180 or 162. Corequisite: 306
{Offered upon demand}
MATH 309 / 509.
Applications of Mathematics.
(3)
An experience in mathematical invention and discovery at the level of high school geometry and algebra that includes a deeper look at sequences, series, and recursions. (T)
Prerequisite: 181 or 163
MATH 311.
Vector Analysis.
(3)
Vector algebra, lines, planes; vector valued functions, curves, tangent lines, arc length, line integrals; directional derivative and gradient; divergence, curl, Gauss’ and Stokes’ theorems, geometric interpretations.
Prerequisite: 264
MATH **312.
Partial Differential Equations for Engineering.
(3)
Solution methods for partial differential equations; science and engineering applications; heat and wave equations, Laplace’s equation; separation of variables; Fourier series and transforms; special functions.
Prerequisite: 264 and 316
MATH **313.
Complex Variables for Engineering.
(3)
Theory of functions of a complex variable with application to physical and engineering problems. Although not required, skill in vector analysis will be helpful in taking this course.
Prerequisite: 264
MATH **314.
Linear Algebra with Applications.
(3)
Note: See Restrictions earlier in Mathematics and Statistics.
System of linear equations, matrices, linear transformations, determinants, eigenvalues and eigenvectors. Efficient computational methods emphasized.
Prerequisite: (163 or 181) and CS 151L
MATH **316.
Applied Ordinary Differential Equations.
(3)
Introduction to algorithmic theory of ordinary differential equations. Topics covered: elementary theory of ordinary differential equations, numerical methods, phase-plane analysis, and introduction to Laplace transformations. Third-level calculus is helpful for this class.
Prerequisite: 163 and CS 151L
MATH **317.
Elementary Combinatorics.
(3)
Basic enumeration including combinations, permutations, set and integer partitions, distributions, and rearrangements, binomial and multinomial theorems together with pigeon-hole and inclusion-exclusion principles and mathematical induction principles. Discrete probability, elementary ordinary generating functions, recurrence relations, and sorting algorithms.
Prerequisite: 163 or 181
{Fall}
MATH **318.
Graph Theory.
(3)
Trees, connectivity, planarity, colorability, and digraphs; algorithms and models involving these concepts. Ability in linear algebra is helpful when taking this course.
{Spring}
MATH **319.
Theory of Numbers.
(3)
Divisibility, congruences, primitive roots, quadratic residues, diophantine equations, continued fractions, partitions, number theoretic functions.
{Spring}
MATH **321.
Linear Algebra.
(3)
Note: See Restrictions earlier in Mathematics and Statistics.
Linear transformations, matrices, eigenvalues and eigenvectors, inner product spaces.
Prerequisite: 264
{Fall, Spring}
MATH 322.
Modern Algebra I.
(3)
Groups, rings, homomorphisms, permutation groups, quotient structure, ideal theory, fields.
Prerequisite: 264
{Fall}
MATH **327.
Introduction to Mathematical Thinking and Discrete Structures.
(3)
Course will introduce students to the fundamentals of mathematical proof in the context of discrete structures. Topics include logic, sets and relations, functions, integers, induction and recursion, counting, permutations and combinations and algorithms.
Prerequisite: 162 and 163
(Fall)
MATH 338 / 542.
Mathematics for Secondary Teachers.
(3)
Topics from secondary mathematics presented from an advanced standpoint and designed to meet the needs of pre- and in-service teachers. Open only to prospective and in-service teachers of mathematics. (T)
Prerequisite: 306 and 327
{Spring}
MATH 339 / 543.
Topics in Mathematics for Elementary and Middle School Teachers.
(1-3, no limit Δ)
Presents mathematical topics of concern to elementary and mid-school teachers. Open only to in-service and prospective teachers. (T)
{Offered upon demand}
MATH 350 / 550.
Topics in Mathematics for Secondary Teachers.
(1-3, no limit Δ)
Presents mathematical topics of concern to secondary teachers. Open only to in-service and prospective teachers. (T)
{Offered upon demand}
MATH **356.
Symbolic Logic.
(4)
(Also offered as PHIL 356)
This is a first course in logical theory. Its primary goal is to study the notion of logical entailment and related concepts, such as consistency and contingency. Formal systems are developed to analyze these notions rigorously.
MATH **375.
Introduction to Numerical Computing.
(3)
(Also offered as CS 375)
An introductory course covering such topics as solution of linear and nonlinear equations; interpolation and approximation of functions, including splines; techniques for approximate differentiation and integration; solution of differential equations; familiarization with existing software.
Prerequisite: CS 151L
MATH 391.
Advanced Undergraduate Honors Seminar.
(1-3 to a maximum of 8 Δ)
Advanced problem solving. Especially recommended for students wishing to participate in the Putnam Intercollegiate Mathematical Competition.
Restriction: permission of instructor
{Offered upon demand}
MATH 393.
Topics in Mathematics.
(3, no limit Δ)
Selected topics from analysis, algebra, geometry, statistics, model building, interdisciplinary studies and problem solving.
{Offered upon demand}
MATH 401 / **501.
Advanced Calculus I.
(4)
Rigorous treatment of calculus in one variable. Definition and topology of real numbers, sequences, limits, functions, continuity, differentiation and integration. Students will learn how to read, understand and construct mathematical proofs.
Prerequisite: 264 and two courses at the 300+ level.
MATH 402 / **502.
Advanced Calculus II.
(3)
Generalization of 401/501 to several variables and metric spaces: sequences, limits, compactness and continuity on metric spaces; interchange of limit operations; series, power series; partial derivatives; fixed point, implicit and inverse function theorems; multiple integrals.
Prerequisite: 401
MATH **412.
Nonlinear Dynamics and Chaos.
(3)
Qualitative study of linear and nonlinear ordinary differential equations and discrete time maps including stability analysis, bifucations, fractal structures and chaos; applications to biology, chemistry, physics and engineering.
Prerequisite: 264 and (314 or 321) or 316
MATH **415.
History and Philosophy of Mathematics.
(3)
(Also offered as PHIL *415)
A historical survey of principal issues and controversies on the nature of mathematics. Emphasis varies from year to year.
Prerequisite: 163 or 181 or 356
MATH *421.
Modern Algebra II.
(3)
Theory of fields, algebraic field extensions and Galois theory for fields of characteristic zero.
Prerequisite: 322 or 422
{Spring}
MATH **422.
Modern Algebra for Engineers.
(3)
Groups, rings and fields. (This course will not be counted in the hours necessary for a mathematics major.)
Prerequisite: 264
{Fall}
MATH *431 / 535.
Introduction to Topology.
(3)
Metric spaces, topological spaces, continuity, algebraic topology.
Prerequisite: 401
{Fall}
MATH 434 / 534.
Introduction to Differential Geometry.
(3)
Elementary theory of surfaces, differential forms, integral geometry and Riemannian geometry.
Prerequisite: 311 or 402
{Offered upon demand}
MATH **439.
Topics in Mathematics.
(1-3, no limit Δ)
MATH 441.
Probability.
(3)
(Also offered as STAT 461/561)
Mathematical models for random experiments, random variables, expectation. The common discrete and continuous distributions with application. Joint distributions, conditional probability and expectation, independence. Laws of large numbers and the central limit theorem. Moment generating functions.
Prerequisite: MATH 264
{Fall}
MATH 462 / 512.
Introduction to Ordinary Differential Equations.
(3)
Linear systems. Existence and uniqueness theorems, flows, linearized stability for critical points, stable manifold theorem. Gradient and Hamiltonian systems. Limit sets, attractors, periodic orbits, Floquet theory and the Poincare Map. Introduction to perturbation theory.
Prerequisite: (314 or 321) and 316 and 401
{Fall}
MATH 463 / 513.
Introduction to Partial Differential Equations.
(3)
Classification of partial differential equations; properly posed problems; separation of variables, eigenfunctions and Green’s functions; brief survey of numerical methods and variational principles.
Prerequisite: 312 and 313 and (314 or 321) and (311 or 402)
{Spring}
MATH 464 / 514.
Applied Matrix Theory.
(3)
Determinants; theory of linear equations; matrix analysis of differential equations; eigenvalues, eigenvectors and canonical forms; variational principles; generalized inverses.
Prerequisite: 314 or 321
{Fall}
MATH *466.
Mathematical Methods in Science and Engineering.
(3)
Special functions and advanced mathematical methods for solving differential equations, difference equations and integral equations.
Prerequisite: 311 and 312 and 313 and 316
{Spring}
MATH *471.
Introduction to Scientific Computing.
(3)
(Also offered as CS 471)
Introduction to scientific computing fundamentals, exposure to high performance programming language and scientific computing tools, case studies of scientific problem solving techniques.
MATH 472 / 572.
Fourier Analysis and Wavelets.
(3)
Discrete Fourier and Wavelet Transform. Fourier series and integrals. Expansions in series of orthogond wavelets and other functions. Multiresolution and time/frequency analysis. Applications to signal processing and statistics.
Prerequisite: (314 or 321) or 401
{Offered upon demand}
MATH 499.
Individual Study.
(1-3 to a maximum of 6 Δ)
Guided study, under the supervision of a faculty member, of selected topics not covered in regular courses.
MATH 500 / 300.
Computing in the Mathematics Curriculum.
(3)
Use of computers and graphing utilities in the mathematics classroom. Introduction to hardware and commercial software. Applications of selected programming languages to the teaching of mathematics.
Prerequisite: 162 or 181
Restriction: College of Education graduate students
MATH **501/ 401.
Advanced Calculus I.
(4)
Rigorous treatment of calculus in one variable. Definition and topology of real numbers, sequences, limits, functions, continuity, differentiation and integration. Students will learn how to read, understand and construct mathematical proofs.
Prerequisite: 264 and two courses at the 300+ level.
Restriction: College of Education graduate students.
MATH **502 / 402.
Advanced Calculus II.
(3)
Generalization of 401/501 to several variables and metric spaces: sequences, limits, compactness and continuity on metric spaces; interchange of limit operations; series, power series; partial derivatives; fixed point, implicit and inverse function theorems; multiple integrals.
Prerequisite: 501
Restriction: College of Education graduate students.
MATH 503 / 301.
Calculus for Teachers.
(3)
A penetrating look at functions, derivatives, integrals, and the Fundamental Theorem of Calculus that makes explicit how topics in the secondary school curriculum come to fruition in this foundational subject.
Restriction: permission of instructor
MATH 504.
Introductory Numerical Analysis: Numerical Linear Algebra.
(3)
(Also offered as CS 575)
Direct and iterative methods of the solution of linear systems of equations and least squares problems. Error analysis and numerical stability. The eigenvalue problem. Descent methods for function minimization, time permitting.
Prerequisite: 464, 514
{Spring}
MATH 505.
Introductory Numerical Analysis: Approximation and Differential Equations.
(3)
(Also offered as CS 576)
Numerical approximation of functions. Interpolation by polynomials, splines and trigonometric functions. Numerical integration and solution of ordinary differential equations. An introduction to finite difference and finite element methods, time permitting.
Prerequisite: 316, 401
{Fall}
MATH 506 / 306.
College Geometry.
(3)
An axiomatic approach to fundamentals of geometry, both Euclidean and non-Euclidean. Emphasis on historical development of geometry.
Restriction: College of Education graduate students
{Spring}
MATH 507 / 305.
Mathematics from a Historical Perspective.
(3)
A survey of mathematical developments prior to 1800; emphasis on problem solving techniques; comparison of older and more modern methods.
Prerequisite: 163
Restriction: College of Education graduate students
{Fall}
MATH 508 / 308.
Theory and Practice of Problem Solving.
(3)
An experience in mathematical invention and discovery at the level of high school geometry and algebra that includes a deeper look at sequences, series, and recursions.
Prerequisite: 180 or 162. Corequisite: 306
Restriction: College of Education graduate students
{Offered upon demand}
MATH 509 / 309.
Applications of Mathematics.
(3)
An experience in mathematical invention and discovery at the level of high school geometry and algebra that includes a deeper look at sequences, series, and recursions.
Prerequisite: 181 or 163
Restriction: College of Education graduate students
MATH 510.
Introduction to Analysis I.
(3)
Real number fields, sets and mappings. Basic point set topology, sequences, series, convergence issues. Continuous functions, differentiation, Riemann integral. General topology and applications: Weierstrass and Stone-Weierstrass approximation theorems, elements of Founier Analysis (time permitting).
Prerequisite: 321, 401
{Fall}
MATH 511.
Introduction to Analysis II.
(3)
Continuation of 510. Differentiation in Rn. Inverse and implicit function theorems, integration in Rn, differential forms and Stokes theorem.
Prerequisite: 510
{Spring}
MATH 512 / 462.
Introduction to Ordinary Differential Equations.
(3)
Linear systems. Existence and uniqueness theorems, flows, linearized stability for critical points, stable manifold theorem. Gradient and Hamiltonian systems. Limit sets, attractors, periodic orbits, Floquet theory and the Poincare Map. Introduction to perturbation theory.
Prerequisite: 314, or 321, 316, 401
{Fall}
MATH 513 / 463.
Introduction to Partial Differential Equations.
(3)
Classification of partial differential equations; properly posed problems; separation of variables, eigenfunctions and Green’s functions; brief survey of numerical methods and variational principles.
Prerequisite: 312, 313, 314 or 321, one of 311 or 402
{Spring}
MATH 514 / 464.
Applied Matrix Theory.
(3)
Determinants; theory of linear equations; matrix analysis of differential equations; eigenvalues, eigenvectors and canonical forms; variational principles; generalized inverses.
Prerequisite: 314 or 321
{Fall}
MATH 519.
Selected Topics in Number Theory.
(3, no limit Δ)
MATH 520.
Abstract Algebra I.
(3)
Theory of groups, permutation groups, Sylow theorems. Introduction to ring theory, polynomial rings. Principal ideal domains.
Prerequisite: 322
{Fall}
MATH 521.
Abstract Algebra II.
(3)
Continuation of 520. Module theory, field theory, Galois theory.
Prerequisite: 321, 520
{Spring}
MATH 530.
Algebraic Geometry I.
(3)
Basic theory of complex affine and projective varieties. Smooth and singular points, dimension, regular and rational mappings between varieties, Chow’s theorem.
Prerequisite: 431, 521, 561
{Alternate Falls}
MATH 531.
Algebraic Geometry II.
(3)
Continuation of 530. Degree of a variety and linear systems. Detailed study of curves and surfaces.
Prerequisite: 530
{Alternate Springs}
MATH 532.
Algebraic Topology I.
(3)
Introduction to homology and cohomology theories. Homotopy theory, CW complexes.
Prerequisite: 431, 521
{Alternate Falls}
MATH 533.
Algebraic Topology II.
(3)
Continuation of 532. Duality theorems, universal coefficients, spectral sequence.
Prerequisite: 532
{Alternate Springs}
MATH 534 / 434.
Introduction to Differential Geometry.
(3)
Elementary theory of surfaces, differential forms, integral geometry and Riemannian geometry.
Prerequisite: 311 or 402
{Offered upon demand}
MATH 535 / 431.
Foundations of Topology.
(3)
Basic point set topology. Separation axioms, metric spaces, topological manifolds, fundamental group and covering spaces.
Prerequisite: 401
{Fall}
MATH 536.
Introduction to Differentiable Manifolds.
(3)
Concept of a manifold, differential structures, vector bundles, tangent and cotangent bundles, embedding, immersions and submersions, transversality, Stokes’ theorem.
Prerequisite: 511
{Spring}
MATH 537.
Riemannian Geometry I.
(3)
Theory of connections, curvature, Riemannian metrics, Hopf-Rinow theorem, geodesics. Riemannian submanifolds.
Prerequisite: 536
{Alternate Falls}
MATH 538.
Riemannian Geometry II.
(3)
Continuation of MATH 537 with emphasis on adding more structures. Riemannian submersions, Bochner theorems with relation to topology of manifolds, Riemannian Foliations, Complex and Kaehler geometry, Sasakian and contact geometry.
Prerequisite: 537
{Alternate Springs}
MATH 539.
Selected Topics in Geometry and Topology.
(3, no limit Δ)
MATH 540.
Stochastic Processes with Applications.
(3)
(Also offered as STAT 565)
Markov chains and processes with applications. Classification of states. Decompositions. Stationary distributions. Probability of absorption, the gambler’s ruin and mean time problems. Queuing and branching processes. Introduction to continuous time Markov processes. Jump processes and Brownian motion.
Prerequisite: STAT 527
{Offered on demand}
MATH 541.
Advanced Probability.
(3)
(Also offered as STAT 567)
A measure theoretic introduction to probability theory. Construction of probability measures. Distribution and characteristic functions, independence and zero-one laws. Sequences of independent random variables, strong law of large numbers and central limit theorem. Conditional expectation. Martingales.
Prerequisite: 563
{Alternate Springs}
MATH 542 / 338.
Mathematics for Secondary Teachers.
(3)
Topics from secondary mathematics presented from an advanced standpoint and designed to meet the needs of pre- and in-service teachers. Open only to prospective and in-service teachers of mathematics.
Restriction: College of Education graduate students
Prerequisite: 306 and 322 and 327
{Fall}
MATH 543 / 339.
Topics in Mathematics for Elementary and Middle School Teachers.
(1-3, no limit Δ)
Presents mathematical topics of concern to elementary and mid-school teachers. Open only to in-service and prospective teachers. May be repeated for credit by permission of instructor.
Restriction: College of Education graduate students
{Offered upon demand}
MATH 549.
Selected Topics in Probability Theory.
(3, no limit Δ)
(Also offered as STAT 569)
MATH 350 / 550.
Topics in Mathematics for Secondary Teachers.
(1-3, no limit Δ)
Presents mathematical topics of concern to secondary teachers. Open only to in-service and prospective teachers. May be repeated for credit by permission of instructor.
Restriction: College of Education graduate students
{Offered upon demand}
MATH 551.
Problems.
(1-3, no limit Δ)
MATH 557.
Selected Topics in Numerical Analysis.
(3, no limit Δ)
(Also offered as CS 557)
Possible topics include approximation theory, two point boundary value problems, quadrature, integral equations and roots of nonlinear equations.
MATH 561.
Functions of a Complex Variable I.
(3)
Analyticity, Cauchy theorem and formulas, Taylor and Laurent series, singularities and residues, conformal mapping, selected topics.
Prerequisite: 311 or 402
{Fall}
MATH 562.
Functions of a Complex Variable II.
(3)
The Mittag-Leffler theorem, series and product expansions, introduction to asymptotics and the properties of the gamma and zeta functions. The Riemann mapping theorem, harmonic functions and Dirichlet’s problem. Introduction to elliptic functions. Selected topics.
Prerequisite: 561
{Fall}
MATH 563.
Measure Theory.
(3)
Functions of one and several real variables, measure theory, starting with Lebesque measure and integration. Product measures. Measure on spaces of functions.
Prerequisite: 401 or 510
{Fall}
MATH 565.
Harmonic Analysis.
(3)
Fourier analysis on the circle, real line and on compact and locally compact groups.
Prerequisite: 563
{Offered upon demand}
MATH 568.
Stochastic Differential Equations.
(3)
Basic theory of stochastic differential equations with applications. The presentation will be at a level accessible to scientists, engineers and applied mathematicians.
Prerequisite: 316 and 441
{Offered upon demand}
MATH 569.
Selected Topics in Analysis.
(3, no limit Δ)
MATH 570.
Singular Perturbations.
(3)
Singularly perturbed boundary value problems, layer type expansions and matching. Initial value problems and multiscaling methods for ordinary and partial differential equations. Phase plane and qualitative ideas. Applications. Perturbations of Hamiltonian systems.
Prerequisite: 462, 463
{Alternate Springs}
MATH 571.
Ordinary Differential Equations.
(3)
Existence and uniqueness of solutions, linear systems, asymptotic behavior of solutions to nonlinear systems, integral manifolds and linearizations, perturbation theory, bifurcation theory, dichotomies for solutions of linear systems.
Prerequisite: 462
{Alternate Springs}
MATH 572 / 472.
Fourier Analysis and Wavelets.
(3)
Discrete Fourier and Wavelet Transform. Fourier series and integrals. Expansions in series of orthogond wavelets and other functions. Multiresolution and time/frequency analysis. Applications to signal processing and statistics.
Prerequisite: 314, 321 or 401
{Offered upon demand}
MATH 573.
Partial Differential Equations.
(3)
Equations of first order, classification of equations and systems, elliptic equations and introduction to potential theory, hyperbolic equations and systems, parabolic equations.
Prerequisite: 463
{Alternate Falls}
MATH 576.
Numerical Linear Algebra.
(3)
Selected advanced topics in numerical linear algebra.
Prerequisite: 504
{Alternate Springs}
MATH 577.
Numerical Ordinary Differential Equations.
(3)
Numerical methods for initial value and/or boundary value problems.
Prerequisite: 462, 504, 505
{Offered upon demand}
MATH 578.
Numerical Partial Differential Equations.
(3)
Introduction to the numerical analysis of partial differential equations.
Prerequisite: 463, 504, 505
{Alternate Falls}
MATH 579.
Selected Topics in Applied Mathematics.
(3, no limit Δ)
MATH 581.
Functional Analysis I.
(3)
Normed vector spaces, including Hilbert and Banach spaces. Linear operators on these spaces, with an emphasis on applications.
Prerequisite: 510
{Offered upon demand}
MATH 582.
Functional Analysis II.
(3)
Advanced topics in function spaces and linear operators.
Prerequisite: 581
MATH 583.
Methods of Applied Mathematics I.
(3)
Approximation in Hilbert spaces, basic operator theory, integral equations, distribution theory, Green’s functions, differential operators, boundary value problems and nonlinear problems.
Prerequisite: 312, 314, 316, 401
{Alternate Falls}
MATH 584.
Methods of Applied Mathematics II.
(3)
Eigenfunction expansions for ordinary and partial differential operators, Euler-Lagrange equations, Hamilton’s principle, calculus of variations, brief complex variable theory, special functions, transform and spectral theory, asymptotic expansions.
Prerequisite: 312 and 314 and 316 and 401
{Alternate Springs}
MATH 598.
Practicum.
(1-6 to a maximum of 6 Δ)
Practicum involves a project of an applied nature which may be done in conjunction with an industrial laboratory, a research institution or another department of the University. It is expected the student will become acquainted with a field of application in science or engineering and complete a project of use and interest to workers in that field. A final written report is required.
MATH 599.
Master’s Thesis.
(1-6, no limit Δ)
Offered on a CR/NC basis only.
MATH 605.
Graduate Colloquium.
(1 to a maximum of 4 Δ)
Students present their current research.
MATH 639.
Seminar in Geometry and Topology.
(1-3, no limit Δ)
MATH 649.
Seminar in Probability and Statistics.
(1-3, no limit Δ)
(Also offered as STAT 649)
MATH 650.
Reading and Research.
(1-6 to a maximum of 12 Δ)
MATH 669.
Seminar in Analysis.
(1-3, no limit Δ)
MATH 679.
Seminar in Applied Mathematics.
(1-3, no limit Δ)
MATH 689.
Seminar in Functional Analysis.
(1-3)
MATH 699.
Dissertation.
(3-12, no limit Δ)
Offered on a CR/NC basis only.
STAT 145.
Introduction to Statistics.
(3)
Techniques for the visual presentation of numerical data, descriptive statistics, introduction to probability and basic probability models used in statistics, introduction to sampling and statistical inference, illustrated by examples from a variety of fields.
Prerequisite: ACT = >22 or SAT = >510 or MATH 120 or 121 or 123 or 150 or 162 or 163 or 180 or 181 or 264.
{Summer, Fall, Spring}
STAT **345.
Elements of Mathematical Statistics and Probability Theory.
(3)
An introduction to probability including combinatorics, Bayes’ theorem, probability densities, expectation, variance and correlation. An introduction to estimation, confidence intervals and hypothesis testing.
Prerequisite: MATH 181 or MATH 163
STAT 425 / 525.
SAS® Programming.
(3)
A detailed introduction to the SAS® programming language. Topics covered include reading data, storing data, manipulating data, data presentation, graphing, and macro programming. SAS® software will be used.
Prerequisite: 345 and 427
STAT 427 / **527.
Advanced Data Analysis I.
(3)
Statistical tools for scientific research, including parametric and non-parametric methods for ANOVA and group comparisons, simple linear and multiple linear regression, and basic ideas of experimental design and analysis. Emphasis placed on the use of statistical packages such as Minitab® and SAS®.
Prerequisite: 145
{Fall}
STAT 428 / 528.
Advanced Data Analysis II.
(3)
A continuation of 427 that focuses on methods for analyzing multivariate data and categorical data. Topics include MANOVA, principal components, discriminant analysis, classification, factor analysis, analysis of contingency tables including log-linear models for multidimensional tables and logistic regression.
Prerequisite: 427
STAT 434 / 534.
Contingency Tables and Dependence Structures.
(3)
This course examines the use of log-linear models to analyze count data. It also uses graphical models to examine dependence structures for both count data and measurement data.
Prerequisite: 345 and 427
STAT 440 / 540.
Regression Analysis.
(3)
Simple regression and multiple regression. Residual analysis and transformations. Matrix approach to general linear models. Model selection procedures, nonlinear least squares, logistic regression. Computer applications.
Prerequisite: 427
{Fall}
STAT 445 / 545.
Analysis of Variance and Experimental Design.
(3)
A data-analytic course. Multifactor ANOVA. Principles of experimental design. Analysis of randomized blocks, Latin squares, split plots, etc. Random and mixed models. Extensive use of computer packages with interpretation, diagnostics.
Prerequisite: 440
{Spring}
STAT 453 / 553.
Statistical Inference with Applications.
(3)
Transformations of univariate and multivariate distributions to obtain the special distributions important in statistics. Concepts of estimation and hypothesis testing in both large and small samples with emphasis on the statistical properties of the more commonly used procedures, including student’s t-tests, F-tests and chi-square tests. Confidence intervals. Performance of procedures under non-standard conditions (i.e., robustness).
Prerequisite: 461
{Spring}
STAT 461 / 561.
Probability.
(3)
(Also offered as MATH 441)
Mathematical models for random experiments, random variables, expectation. The common discrete and continuous distributions with application. Joint distributions, conditional probability and expectation, independence. Laws of large numbers and the central limit theorem. Moment generating functions.
Prerequisite: MATH 264
{Fall}
STAT 470 / 570.
Industrial Statistics.
(3)
Basic ideas of statistical quality control and improvement. Topics covered: Deming’s 14 points and deadly diseases, Pareto charts, histograms, cause and effect diagrams, control charts, sampling, prediction, reliability, experimental design, fractional factorials, Taguchi methods, response surfaces.
Prerequisite: 345
STAT 472 / 572.
Sampling Theory and Practice.
(3)
Basic methods of survey sampling; simple random sampling, stratified sampling, cluster sampling, systematic sampling and general sampling schemes; estimation based on auxiliary information; design of complex samples and case studies.
Prerequisite: 345
{Alternate Falls}
STAT 474 / 574.
Biostatistical Methods: Survival Analysis and Logistic Regression.
(3)
A detailed overview of methods commonly used to analyze medical and epidemiological data. Topics include the Kaplan-Meier estimate of the survivor function, models for censored survival data, the Cox proportional hazards model, methods for categorical response data including logistic regression and probit analysis, generalized linear models.
Prerequisite: 428 or 440
STAT 476 / 576.
Multivariate Analysis.
(3)
Tools for multivariate analysis including multivariate ANOVA, principal components analysis, discriminant analysis, cluster analysis, factor analysis, structural equations modeling, canonical correlations and multidimensional scaling.
Prerequisite: 428 or 440
{Offered upon demand}
STAT 477 / 577.
Introduction to Bayesian Modeling.
(3)
An introduction to Bayesian methodology and applications. Topics covered include: probability review, Bayes’ theorem, prior elicitation, Markov chain Monte Carlo techniques. The free software programs WinBUGS and R will be used for data analysis.
Prerequisite: 461 and (427 or 440)
{Alternate Springs}
STAT 479.
Topics in Statistics.
(3, no limit Δ)
Modern topics not covered in regular course offerings.
STAT 481 / 581.
Introduction to Time Series Analysis.
(3)
Introduction to time domain and frequency domain models of time series. Data analysis with emphasis on Box-Jenkins methods. Topics such as multivariate models; linear filters; linear prediction; forecasting and control.
Prerequisite: 461
{Alternate Springs}
STAT 495.
Individual Study.
(1-3 to a maximum of 6 Δ)
Guided study, under the supervision of a faculty member, of selected topics not covered in regular course offerings.
STAT 520.
Topics in Interdisciplinary Biological and Biomedical Sciences.
(3, unlimited Δ)
(Also offered as ANTH 620, BIOL 520, CS 520, ECE 620)
Varying interdisciplinary topics taught by collaborative scientists from UNM, SFI, and LANL.
STAT 524.
Collaborative Interdiciplinary Teaching.
(3)
(Also offered as BIOL 524, CS 524, ANTH 624, ECE 524)
Course designed to develop the methods content and assessment of effective interdisciplinary biological courses; Students will develop and teach an undergraduate interdisciplinary topics course. Topics vary.
Restriction: permission of instructor.
STAT 525 / 425.
SAS® Programming.
(3)
A detailed introduction to the SAS® programming language. Topics covered include reading data, storing data, manipulating data, data presentation, graphing, and macro programming. SAS® software will be used.
Prerequisite: 345, 427
STAT **527 / 427.
Advanced Data Analysis I.
(3)
Statistical tools for scientific research, including parametric and non-parametric methods for ANOVA and group comparisons, simple linear and multiple linear regression and basic ideas of experimental design and analysis. Emphasis placed on the use of statistical packages such as Minitab® and SAS®. Course cannot be counted in the hours needed for graduate degrees in Mathematics and Statistics.
Prerequisite: 145
{Fall}
STAT 528 / 428.
Advanced Data Analysis II.
(3)
A continuation of 527 that focuses on methods for analyzing multivariate data and categorical data. Topics include MANOVA, principal components, discriminate analysis, classification, factor analysis, analysis of contingency tables including log-linear models for multidimensional tables and logistic regression.
Prerequisite: 527
STAT 531.
Statistical Genetics I.
(3)
A detailed examination of the statistical methods used in analyzing genetic data. Topics covered include the estimation of allele frequencies, testing for Hardy-Weinberg equilibrium, classical and complex segregation analysis, linkage analysis for Mendelian and complex diseases, and the detection of allelic association. Popular genetic software will be used for data analysis.
Prerequisite: 345, 427
{Alternate Falls}
STAT 532.
Statistical Genetics II.
(3)
A continuation of 531. Topics covered include statistical methods for describing variation in quantitative traits, methods of mapping and characterizing quantitative trait loci and other current topics in statistical genetics, including the analysis of microarray data and phylogenetic methods. Popular genetic software will be used for data analysis.
Prerequisite: 531
{Alternate Springs}
STAT 534 / 434.
Contingency Tables and Dependence Structures.
(3)
This course examines the use of log-linear models to analyze count data. It also uses graphical models to examine dependence structures for both count data and measurement data.
Prerequisite: 345, 427
STAT **538.
Biostatistical Methods I for Public Health and Medical Sciences.
(3)
Covers basic statistical methods including statistical summaries and inference. Methods of summarizing data include graphical displays and numerical summaries. Statistical inference includes hypothesis testing and confidence intervals. Methods for continuous and categorical data are studied.
Prerequisite: B or better in MATH 121
{Fall}
STAT **539.
Biostatistical Method II for Public Health and Medical Sciences.
(3)
Covers basic models used in the statistical analysis of studies in the medical sciences and public health field, with an emphasis on epidemiology. Linear regression, analysis of variance, logistic regression, and survival models are studied.
Prerequisite: 538
{Spring}
STAT 540 / 440.
Regression Analysis.
(3)
Simple regression and multiple regression. Residual analysis and transformations. Matrix approach to general linear models. Model selection procedures, nonlinear least squares, logistic regression. Computer applications.
Prerequisite: 527
{Fall}
STAT 545 / 445.
Analysis of Variance and Experimental Design.
(3)
A data-analytic course. Multifactor ANOVA. Principles of experimental design. Analysis of randomized blocks, Latin squares, split plots, etc. Random and mixed models. Extensive use of computer packages with interpretation, diagnostics.
Prerequisite: 540
{Spring}
STAT 546.
Theory of Linear Models.
(3)
Theory of the Linear Models discussed in 440/540 and 445/545. Linear spaces, matrices, projections, multivariate normal distribution and theory of quadratic forms. Non-full rank models and estimability. Gauss-Markov theorem. Distribution theory for normality assumptions. Hypothesis testing and confidence regions.
Prerequisite: 553, 545, linear algebra.
{Alternate Falls}
STAT 547.
Multivariate Analysis and Advanced Linear Models.
(3)
Hotelling T2, multivariate ANOVA and Regression, classification and discrimination, principal components and factor analysis, clustering, graphical and computational techniques, topics in linear models.
Prerequisite: 546
{Alternate Springs}
STAT 553 / 453.
Statistical Inference with Applications.
(3)
Transformations of univariate and multivariate distributions to obtain the special distributions important in statistics. Concepts of estimation and hypothesis testing in both large and small samples with emphasis on the statistical properties of the more commonly used procedures, including student’s t-tests, F-tests and chi-square tests. Confidence intervals. Performance of procedures under non-standard conditions (i.e., robustness).
Prerequisite: 561
{Spring}
STAT 556.
Advanced Statistical Inference I.
(3)
Theory and methods of point estimation, sufficiency and its applications.
Prerequisite: 553, 561 and MATH 510
{Alternate Falls}
STAT 557.
Advanced Statistical Inference II.
(3)
Standard limit theorems, hypothesis testing, confidence intervals and decision theory.
Prerequisite: 556
{Alternate Springs}
STAT 561 / 461.
Probability.
(3)
Mathematical models for random experiments, random variables, expectation. The common discrete and continuous distributions with application. Joint distributions, conditional probability and expectation, independence. Laws of large numbers and the central limit theorem. Moment generating functions.
Prerequisite: MATH 264
{Fall}
STAT 565.
Stochastic Processes with Applications.
(3)
(Also offered as MATH 540)
Markov chains and processes with applications. Classification of states. Decompositions. Stationary distributions. Probability of absorption, the gambler’s ruin and mean time problems. Queuing and branching processes. Introduction to continuous time Markov processes. Jump processes and Brownian motion.
Prerequisite: 561
{Offered on demand}
STAT 567.
Advanced Probability.
(3)
(Also offered as MATH 541)
A measure theoretic introduction to probability theory. Construction of probability measures. Distribution and characteristic functions, independence and zero-one laws. Sequences of independent random variables, strong law of large numbers and central limit theorem. Conditional expectation. Martingales.
Prerequisite: MATH 563
{Alternate Springs}
STAT 569.
Selected Topics in Probability Theory.
(3, no limit Δ)
(Also offered as MATH 549)
STAT 570 / 470.
Industrial Statistics.
(3)
Basic ideas of statistical quality control and improvement. Topics covered: Deming’s 14 points and deadly diseases, Pareto charts, histograms, cause and effect diagrams, control charts, sampling, prediction, reliability, experimental design, fractional factorials, Taguchi methods, response surfaces.
Prerequisite: 345
STAT 572 / 472.
Sampling Theory and Practice.
(3)
Basic methods of survey sampling; simple random sampling, stratified sampling, cluster sampling, systematic sampling and general sampling schemes; estimation based on auxiliary information; design of complex samples and case studies.
Prerequisite: 345
{Alternate Falls}
STAT 574 / 474.
Biostatistical Methods: Survival Analysis and Logistic Regression.
(3)
A detailed overview of methods commonly used to analyze medical and epidemiological data. Topics include the Kaplan-Meier estimate of the survivor function, models for censored survival data, the Cox proportional hazards model, methods for categorical response data including logistic regression and probit analysis, generalized linear models.
Prerequisite: 528 or 540
STAT 576 / 476.
Multivariate Analysis.
(3)
Tools for multivariate analysis including multivariate ANOVA, principal components analysis, discriminant analysis, cluster analysis, factor analysis, structural equations modeling, canonical correlations and multidimensional scaling.
Prerequisite: 528 or 540
{Offered upon demand}
STAT 577 / 477.
Introduction to Bayesian Modeling.
(3)
An introduction to Bayesian methodology and applications. Topics covered include: probability review, Bayes’ theorem, prior elicitation, Markov chain Monte Carlo techniques. The free software programs WinBUGS and R will be used for data analysis.
Prerequisite: 561 and (527 or 540)
{Alternate Springs}
STAT 579.
Selected Topics in Statistics.
(3, no limit Δ)
STAT 581 / 481.
Introduction to Time Series Analysis.
(3)
Introduction to time domain and frequency domain models of time series. Data analysis with emphasis on Box-Jenkins methods. Topics such as multivariate models; linear filters; linear prediction; forecasting and control.
Prerequisite: 561
{Alternate Springs}
STAT 582.
Advanced Time Series Analysis.
(3)
Time series models in the time and spectral domains. Linear filters. Multivariate models. Autoregressive and moving average models. Filtering and prediction. Distribution theory. Design of experiments.
Prerequisite: 581
{Alternate Falls}
STAT 585.
Nonparametric and Robust Methods.
(3)
Statistical methods that are insensitive to the distribution of the data. Sign tests, Kolmogorov-Smirnov tests, rank tests including the Wilcoxon, Mann-Whitney, Kruskal-Wallis and Friedman tests. Robust estimation including M estimators, L estimators and R estimators.
Prerequisite: 561
{Offered upon demand}
STAT 586.
Nonparametric and Robust Methods.
(3)
Nonparametric regression, density estimation, filtering, spectral density estimation, image reconstruction and pattern recognition. Tools include orthogonal series, kernels, splines, wavelets and neural networks. Applications to medicine, engineering, biostatistics and economics.
Prerequisite: 561
{Offered upon demand}
STAT 590.
Statistical Computing.
(3)
A detailed examination of essential statistical computing skills needed for research and industrial work. Students will use S-Plus, Matlab and SAS® to develop algorithms for solving a variety of statistical problems using resampling and simulation techniques such as the bootstrap, Monte Carlo methods and Markov chain methods for approximating probability distributions. Applications to linear and non-linear models will be stressed.
Prerequisite: 528
STAT 595.
Problems.
(1-3, no limit Δ)
STAT 597.
Statistical Consulting Laboratory.
(1-3, no limit Δ)
Provides experience in statistical consulting and analysis of real data.
Prerequisite: 528
STAT 599.
Master’s Thesis.
(1-6, no limit Δ)
Offered on a CR/NC basis only.
STAT 605.
Graduate Colloquium.
(1 to a maximum of 4 Δ)
Students present their current research.
STAT 649.
Seminar in Probability and Statistics.
(1-3, no limit Δ)
(Also offered as MATH 649)
STAT 650.
Reading and Research.
(1-6 to a maximum of 12 Δ)
STAT 699.
Dissertation.
(3-12, no limit Δ)
Offered on a CR/NC basis only.

![]()
![]()
